Inteligência Artificial
O MSX aprende a jogar
Você está em: MarMSX >> Cursos >> AI
Os métodos apresentados nos capítulos anteriores apresentaram um tipo de inteligência artificial que não é capaz de evoluir, ou seja, aprender algo novo com seus erros ou acertos e agir de uma forma mais adequada a cada situação. Os personagens e jogos agem sempre analisando a situação atual, e tomam uma atitude com base nessa situação. A resposta nesses casos, pode ser através de heurísticas ou ações pré-determinadas.
Que tal fazer com que o MSX aprenda com seus erros e acertos e jogue cada vez melhor?
Um ramo da Inteligência Artificial, chamado de Aprendizado por Reforço (ou Reinforcement Learning em inglês), tem como objetivo fazer com que máquinas ou computadores aprendam através do método de tentativa e erro. Esse método foi inspirado na natureza, onde os animais aprendem através de interações com o meio onde vivem, recebendo um feedback desse meio através de recompensas e punições por suas ações, numa relação causa-efeito.
A idéia central do Aprendizado por Reforço é fazer com que um agente interaja com o meio no qual está inserido, recebendo respostas do meio a cada uma de suas ações, que podem ser positivas (recompensas) ou negativas (punições). Não há um professor ensinando ao aprendiz que ações tomar. Nesse caso, ele deverá aprender através de suas interações com o meio, e ajustar suas ações de forma a maximar o recebimento de recompensas positivas, ou seja, agir de forma correta.
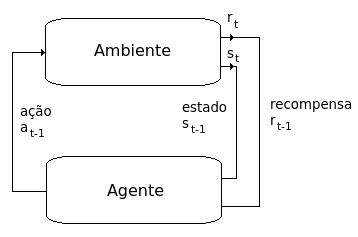
Os outros dois métodos de aprendizagem em Inteligência Artificial são apresentados na seção extra desse curso: o aprendizado supervisionado, onde o computador aprende através de exemplos (professor), e o aprendizado não-supervisionado, onde o computador é capaz de reconhecer padrões nos dados.
Exemplos de Aprendizado por Reforço
Os exemplos apresentados a seguir podem ser encontrados em [1]:
Exemplo 1
Um bezerrinho luta para se manter em pé minutos após seu nascimento. Meia hora depois, está correndo a 30 Km/h.
Exemplo 2
Um robô móvel decide se ele deverá entrar em uma nova sala em busca de mais lixo para coletar ou tentará descobrir o caminho de volta para a estação de recarga de sua bateria. Ele toma sua decisão com base no nível atual de sua bateria e sua experiência passada em encontrar de forma fácil e rápida o cerregador de baterias.
Exemplo 3
Phil prepara seu café da manhã. Ao examinarmos com atenção essa aparente atividade mundana simples, ela revela uma complexa rede de comportamentos condicionais e relacionamentos de metas e sub-metas entrelaçadas:
- Andar até o armário da cozinha
- Abrir o armário
- Escolher um cereal
- Esticar a mão, alcançar e pegar o cereal
Outra complexa seqüência de comportamentos interativos e sincronizados é necessária para se obter a tigela, a colher e o leite. Cada etapa dessas tarefas requer uma série de movimento de olhos, de forma a obter informações e guiar o alcance e a locomoção. Julgamentos rápidos e contínuos são realizados de forma a decidir como carregar os objetos, se é melhor levá-los à mesa antes de se obter os outros. Cada etapa é guiada por objetivos, como pegar uma colher ou ir até a geladeira, e também está a relacionada a outros objetivos, como ter a colher para comer depois de ter preparado o cereal.
Phil está continuamente recebendo informações de seu corpo que indica as necessidades nutricionais, níveis de fome e preferências de comida, independentemente se estiver consciente a tudo isso ou não.
Segundo o livro [1], "nos exemplos apresentados, a interação envolve um agente tomador de decisões e seu meio. As ações do agente alteram o estado futuro do meio, afetando as futuras oportunidades e ações disponíveis para esse agente. A escolha de ações corretas envolve a avaliação das conseqüências de cada ação, geralmente por meio de um planejamento."
"Não é possível realizar a previsão completa dos eventos apresentados. Assim, o agente deverá monitorar frequentemente seu meio e reagir de acordo com a situação. O agente poderá usar sua experiência de forma a melhorar sua performance ao longo do tempo, como,por exemplo, o bezerro fez quando aprendeu a andar."
Elementos do Aprendizado por Reforço
São os principais elementos do Aprendizado por Reforço [1]:
- Agente - Entidade que age e modifica o meio e aprende com seus erros e acertos.
- Meio - Onde o agente atua e modifica o estado.
- Política - define como o agente deve agir em um determinado momento.
- Função-valor - especifica o que é bom a longo prazo (quantidade de recompensas no futuro).
- Sinal de recompensa - define o objetivo do aprendizado por reforço.
- Modelo do ambiente - modela o comportamento do ambiente. Por exemplo, dada uma ação, o modelo prevê o próximo estado e recompensa. Modelos são utilizados para o planejamento de próximas ações por parte do agente.
Estudo de caso - jogo da velha
Segundo o livro [1], devemos seguir seguir os seguintes passos para criar um ambiente de Aprendizado por Reforço para um jogo da velha:
"Primeiramente criamos uma tabela com cada estado possível para o jogo. Cada estado armazena o último valor de probabilidade estimada de vitória, enquanto que a tabela completa é a função-valor aprendida. Um estado A com valor maior que B é considerado uma melhor opção. Um estado que possua todas as pedras do MSX em linha ou diagonal possui probabilidade de vitória igual a 1, enquanto que os estados que possuam todas as pedras do adversário humano em linha ou diagonal possui probabilidade de vitória igual a 0. O mesmo pode se dizer dos estados em que houve empate. Os demais estados são inicialmente ajustados para 0.5, ou seja, 50% de chances de vitória."
Exemplo de estados, supondo o MSX como "O":
O X . X O . O . .
O . . X . . . . .
O X . X O . . . .
P=1.0 P=0.0 P=0.5
"Para o aprendizado se concretizar, devemos jogar diversas partidas contra o adversário humano. Em cada movimento, o computador deverá examinar todos os estados futuros possíveis (espaços livres no tabuleiro) e avaliar a melhor probabilidade de vitória (movimento ganacioso). Entretanto, às vezes é necessário realizar um movimento aleatório chamado de exploratório, para se atingir determinados estados que jamais seriam atingidos."
"A cada jogada em movimentos gananciosos, modificamos o valor do estado atual sempre uma fração na direção do valor do estado futuro. O objetivo disso é tornar as estimativas mais precisas."
V(St) = V(St) + α[V(St+1) - V(St)]
Onde α é a taxa de aprendizado.
No caso do jogo da velha, as recompensas só serão obtidas após o término do jogo: vitória, empate ou derrota. Durante cada etapa de aprendizado (jogo), diversas ações são realizadas de acordo com o conhecimento adquirido.
Programa base do jogo da velha em Basic
O programa base para o jogo da velha é apresentado a seguir.
5 ' MarMSX 2021
10 SCREEN 0:WIDTH 40:KEY OFF:COLOR 15,1,1
20 PRINT"Jogo da Velha":PRINT
30 PRINT" | | "
40 PRINT"---+---+--- Voce: X"
50 PRINT" | | "
60 PRINT"---+---+--- MSX : O"
70 PRINT" | | "
80 PRINT:PRINT"Mova o cursor com as setas"
90 DIM TA(3,3)
100 '
101 ' Inicia jogo
102 '
110 GOSUB 300 ' Limpa tabuleiro
120 X=0:Y=0:TM=0
130 GOSUB 400 ' Desenha pecas
200 '
201 ' Loop principal
202 '
210 LOCATE X*4+1,Y*2+2:K$=INPUT$(1):K=ASC(K$)
220 IF K=31 THEN Y=Y+1:IF Y>2 THEN Y=2
230 IF K=30 THEN Y=Y-1:IF Y<0 THEN Y=0
240 IF K=28 THEN X=X+1:IF X>2 THEN X=2
250 IF K=29 THEN X=X-1:IF X<0 THEN X=0
260 IF K=32 THEN 275
270 GOTO 210
275 GOSUB 500 : IF JV=0 THEN 210 ELSE TM=TM+1
280 GOSUB 600 : IF V<>0 THEN 800
285 GOSUB 1000 : TM=TM+1
290 GOSUB 600 : IF V<>0 THEN 800
295 GOTO 210
300 '
301 ' Limpa tabuleiro
302 '
310 FOR I=1 TO 3 : FOR J=1 TO 3 : TA(I,J)=0 : NEXT J,I
400 '
401 ' Imprime dados do tabuleiro
402 '
410 FOR I=1 TO 3 : FOR J=1 TO 3
420 MK$=" " : IF TA(I,J)=1 THEN MK$="X" ELSE IF TA(I,J)=2 THEN MK$="O"
430 LOCATE (J-1)*4+1,(I-1)*2+2 : PRINT MK$
440 NEXT J,I
450 RETURN
500 '
501 ' Realiza marcacao do jogador
502 '
510 JV=0
520 IF TA(Y+1,X+1)=0 THEN TA(Y+1,X+1)=1 : JV=1 : GOSUB 400
530 RETURN
600 '
601 ' Verifica fim de jogo
602 '
610 V=0 : FOR I=1 TO 3 : JH=0 : MH=0 : JV=0 : MV=0 : FOR J=1 TO 3
620 IF TA(I,J)=1 THEN JH=JH+1
630 IF TA(J,I)=1 THEN JV=JV+1
640 IF TA(I,J)=2 THEN MH=MH+1
650 IF TA(J,I)=2 THEN MV=MV+1
660 IF JH=3 OR JV=3 THEN V=1 : RETURN
670 IF MH=3 OR MV=3 THEN V=2 : RETURN
680 NEXT J,I
700 JH=0 : MH=0 : JV=0 : MV=0 : FOR I=1 TO 3
710 IF TA(I,I)=1 THEN JH=JH+1
720 IF TA(I,I)=2 THEN MH=MH+1
730 IF TA(4-I,I)=1 THEN JV=JV+1
740 IF TA(4-I,I)=2 THEN MV=MV+1
750 NEXT I
760 IF JH=3 OR JV=3 THEN V=1 : RETURN
770 IF MH=3 OR MV=3 THEN V=2 : RETURN
780 IF TM=9 THEN V=3
790 RETURN
800 '
801 ' Fim de jogo
802 '
810 LOCATE 0,12
820 IF V=1 THEN PRINT"Voce venceu o jogo !!" ELSE IF V=2 THEN PRINT"Eu venci o jogo !!" ELSE PRINT"Empate !!"
830 PRINT"Tecle algo para reiniciar ..."
840 A$=INPUT$(1)
850 LOCATE 0,12:PRINT SPC(40):PRINT SPC(40)
860 GOTO 100
Na linha 285 há um desvio para a linha 1000. A partir dessa linha, iremos introduzir diferentes códigos para a inteligência do MSX.
Jogo aleatório
Aqui o MSX joga de qualquer maneira, sempre escolhendo aleatoriamente sua próxima posição. Não há qualquer aprendizado.
1000 '
1001 ' Jogada do MSX - aleatoria
1002 '
1010 CX=INT(RND(-TIME)*3+1):CY=INT(RND(-TIME)*3+1)
1020 IF TA(CX,CY)<>0 THEN 1010 ELSE TA(CX,CY)=2
1030 GOSUB 400 RETURN
1040 RETURN
Proposta do livro Inteligência Artificial em Basic
O livro Inteligência Artificial em Basic [2] propõe a criação de um mapa dinâmico de estados, assinalando com um flag os estados relativos aos últimos movimentos que levaram o MSX à derrota. Nesse caso, o movimento que levou MSX a derrota é bloqueado no respectivo estado, fazendo com que outros movimentos estejam livres para serem realizados. Assim, o MSX vai apendendo ao longo do tempo, otimizando o mapa de estados.
Como funciona isso?
São possíveis 5.478 estados legais em um jogo da velha [3][4], o que torna difícil o armazenamento de todos eles na memória do MSX. Assim, o programa vai criando o mapa de estados dinamicamente, conforme o jogo vai acontecendo.
O programa armazena somente os estados onde é a vez do computador. Lembre-se que no Aprendizado por Reforço, o meio apresenta um novo estado ao agente após uma determinada ação sua, para que este agente realize uma nova ação. Nesse caso, o novo estado vem logo após a jogada do adversário.
Exemplo:
Sequência de jogadas:
O . . O O O O .
X X . -> X X . -> X X X
. . . . . . . . .
Humano MSX Humano
X - Jogador
O - MSX
E os estados apresentados pelo meio ao agente:
Estados armazenados:
O . . O O
X X . -> X X X
. . . . . .
Nenhum conhecimento é adicionado aos estados, até que o jogo termine. Porém, nessa proposta, há somente um tipo de recompensa dada que é a derrota. Com a derrota, o último estado antes da efetivação da derrota é sinalizado com um flag na posição relativa à última jogada, informando que esse movimento é um movimento ruim e que deve ser evitado.
O . . O O
X X . -> X X X
. . . . . .
Estado Fim de
Anterior Jogo
Notificação (D):
O D . O O
X X . -> X X X
. . . . . .
Estado Fim de
Anterior Jogo
No programa do livro, as posições são sempre escolhidas sequencialmente. Caso encontre uma posição ocupada ou proibida, ele escolhe a próxima posição. Porém, também podemos escolher uma posição futura livre aleatoriamente, uma vez que nada sabemos a respeito delas.
O autor [2] também altera a representação da tabela do jogo. Ele converte a matriz para um vetor de números. Na realidade, não é um vetor, e sim um número com 9 dígitos.
1 2 3
4 5 6 fica: 123456789
7 8 9
O valor 0 é utilizado para representar os espaços vazios, enquanto que o valor 1 representa um "X" e o valor 2 um "O". O valor 4 representa um futuro estado "proibido".
Exemplo:
. . O
. X . -> 002010200
O . .
Podemos converter os dados de uma tabela T(x,y) para uma seqüência numérica da seguinte maneira:
10 V=0 : P=8
20 FOR X=1 TO 3 : FOR Y=1 TO 3
30 V = V + T(X,Y) * (10^P)
40 P = P - 1
50 NEXT Y,X
O jogo da velha foi recriado por mim e pode ser baixado aqui. Temos os seguintes arquivos:
- velha2.bas - programa feito em Basic do MSX.
- velha2.c - programa em C que segue a abordagem proposta, escolhendo a primeira posição vazia.
- velha2_rnd.c - programa em C que segue a abordagem proposta, escolhendo aleatoriamente uma posição vazia.
Jogue diversas vezes contra o MSX. Inicialmente, ele jogará muito mal. Entretanto, após alguns jogos, ele começa a mostrar os sinais da evolução.
Considerações
Apesar do autor do livro atribuir esse método como sendo uma abordagem de Sistemas Especialistas, ele está em maior conformidade com o Aprendizado por Reforço. Isto porque, nos Sistemas Especialistas, o conhecimento é modelado por um especialista ou professor. Já no Aprendizado por Reforço, o agente aprende sozinho através de interações com o meio no qual está inserido, com o sucesso ou fracasso de suas ações. Podemos observar isto, quando autor [2] afirma que "o jogo da velha tem como conclusões jogadas que somente se provarão corretas ou erradas posteriormente no jogo". Ninguém diz para o agente o que ele deve fazer. Entretanto, ele aprende sozinho com seu fracasso, marcando como ruim o movimento que o levou à derrota.
Em comparação com a teoria apresentada pelo livro [1], difere por ser apenas capaz de avaliar uma má situação futura imediatamente antes dela. Nesse caso, ele não avalia as chances de vencer, bem como não consegue realizar previsões em estados não imediatamente antes de uma situação de vitória ou derrota.
Jogo com o mapa de probabilidades
Após aprendermos sobre o jogo da velha proposto por [2], utilizaremos alguns conceitos desse jogo para a criação do modelo a seguir, como o modo de codificação dos estados do jogo e a construção dinâmica desses.
Nessa nova abordagem, utilizaremos uma probabilidade de vitória associada a cada estado futuro da máquina, em vez de utilizar um flag indicando um caminho ruim.
Dessa forma, o meio fornece um estado atual St, logo após a jogada do humano. Esse estado possui todos os movimentos futuros possíveis da máquina, no qual irá armazenando pouco a pouco em sua memória os futuros estados St+1 relativos às suas ações, com suas respectivas probabilidades de vitória.
Para determinar qual estado St+1 a máquina deverá assumir, verificamos todos os estados futuros possíveis e assumimos o estado com a maior probabilidade de vitória. Se houver empate, podemos retornar o primeiro valor máximo encontrado ou escolher um aleatoriamente.
Um vez que estamos construindo a memória de estados dinamicamente, caso o estado futuro ainda não exista no banco, assuma o valor 0.5 para a probabilidade e o adicione no banco, caso seja o estado vencedor.
Exemplo de alguns estados armazenados no banco de dados:
Estado P
120000000 0.5
120120000 0.5
122100100 0.0
211200200 1.0
Foi visto que a probabilidade de vitória é UM quando o MSX forma uma linha, é ZERO quando o jogador forma uma linha ou dá empate, e 0.5 nos demais estados.
Quando o MSX toma a decisão de ir para um novo estado, ele atualiza o valor da probabilidade do estado armazenado atual com base no estado armazenado futuro ou da recompensa. Essa atualização não é feita, caso o movimento atual seja exploratório.
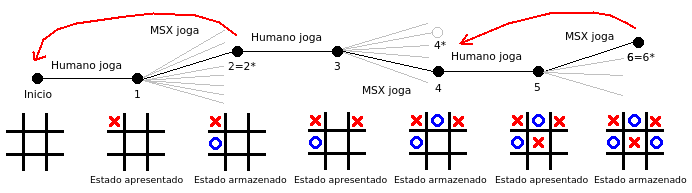 |
| Seqüência de jogadas em um jogo da velha. As linhas cinzas representam as possibilidades de jogadas do MSX, enquanto que as linhas pretas representam as jogadas efetivadas. As setas em vermelho representam a atualização dos estados. Os estados assinalados com o asterisco "*" indicam um movimento ganancioso, enquanto que os sem astericos são movimentos exploratórios. Adapatado de [1].
|
Como estamos construindo o banco de dados dinamicamente, primeiro realizamos o movimento, verificamos a resposta do sistema e depois atualizamos a probabilidade do estado anterior.
P_anterior = P_anterior + α (P_atual - P_anterior)
Exemplo de análise de movimento:
Estado atual:
120100000 0.5
Movimentos possíveis (a partir dos 0's do estado atual):
122100000 0.1
120120000 0.15
120102000 0.2
120100200 0.6
120100020 0.12
120100002 0.1
O melhor movimento é o bloqueio da linha vertical de "X", na posição 3,1 do tabuleiro. Ele possui a maior probabilidade (0.6).
Supondo uma taxa de aprendizado igual a 0.1, temos:
P_atual = 0.5 + 0.1 * (0.6 - 0.5) = 0.5 + 0.01 = 0.51
Assim, temos:
Estado atual:
120100000 0.51
O jogo da velha para essa abordagem pode ser baixado aqui. Temos os seguintes arquivos:
- velha3.bas - programa feito em Basic do MSX. Armazena todos os estados e dispara aprendizado em cascata somente no final.
- velha3.c - programa em C que segue a abordagem proposta, escolhendo o primeiro máximo.
- velha3_rnd.c - programa em C que segue a abordagem proposta, escolhendo aleatoriamente posições máximas.
Alguns ajustes nos programas em C poderão ser feitos. Por exemplo, a taxa de aprendizado alfa possui valor 0.3.
double alpha = 0.3;
Outro ajuste que pode ser feito é na taxa de movimento exploratório. Ela foi ajustada para 30% de movimento exploratório e 70% para movimento de acordo com o aprendizado.
void computer_move()
{
...
srand(time(NULL));
k = rand() % 100;
if (k > 30)
...
}
Altere o valor da expressão "if (k > 30)" de 30 para outro valor, indicando a porcentagem de movimentos exploratórios. Por exemplo, o valor 10 nessa expressão indica que teremos 10% de movimentos exploratórios e 90% de movimentos inteligentes.
O MSX aprendendo contra ele mesmo
Você já deve ter se perguntado se o computador poderia aprender jogando contra ele mesmo. Sim. Nesse caso, poderíamos deixá-lo jogando contra si milhares de vezes, de forma a obter um mapeamento otimizado. Isto é bom, porque o aprendizado poderá ser feito num ritmo muito mais acelerado do que se jogasse contra humanos. Após o aprendizado, podemos salvar o mapa de estados e portá-lo para uma versão do jogo contra humanos.
Em projetos com o Alpha Go da Google, foram necessárias cerca de 29 milhões de partidas dá máquina jogando contra ela mesma para se atingir um bom patamar [5]. Segundo um dos engenheiros do Alpha Go, o autoaprendizado é mais eficiente porque os sistemas enfrentam sempre o mesmo nível de habilidade [5].
Os arquivos "velha2_auto.c" e "velha3_auto.c", feitos em linguagem C, simulam diversas partidas entre o computador jogando contra ele mesmo. Um truque utilizado para o "outro computador" compartilhar seu aprendizado com o computador é a inversão das peças do tabuleiro para a geração de estados, ou seja, para o "outro computador", os X's passam a ser O's e vice-versa.
Após rodar 500, 1000, 5000 partidas, salve os estados e experimente jogar contra a máquina com os programas "velha2.c", "velha2_rnd.c", "velha3.c" e "velha3_rnd.c".
Antes de jogar contra o computador, altere a taxa de movimentos exploratórios de 30% para 10%, conforme visto na seção anterior. Após atingir um certo nível de aprendizagem, não é mais necessário realizar tantos movimentos desse tipo.
Download
ar_data.zip - Programas em Basic do MSX e C.
ar_milhao.zip - Versão do programa "velha3_auto.c" para rodar milhares de vezes com estatística de vitórias, mais um arquivo de dados "auto03.dat" com 1 milhão de partidas realizadas.
Referências:
[1] - Reinforcement Learning: An Introduction, Second Edition. Richard S. Sutton and Andrew G. Barto. Editora The MIT Press, 2020.
[2] - Inteligência Artificial em Basic, M. James, Editora Campus, 1985.
[3] - Game complexity, em: https://en.wikipedia.org/wiki/Game_complexity.
[4] - https://math.stackexchange.com/questions/485752/tictactoe-state-space-choose-calculation
[5] - Aprendizado Profundo para Leigos. John Paul Mueller, Luca Massaron. Editora Alta Books, 2020.


