Inteligência Artificial
Redes Neurais - Feed Forward


Você está em: MarMSX >> Cursos >> AI   Aprendemos no capítulo de aprendizado supervisionado que o perceptron modela um neurônio do cérebro humano. Com ele, vimos que possível fazer com que o computador aprenda, de modo a ser capaz de distinguir entre duas classes linearmente separáveis.
  Para alguns problemas, como por exemplo o ou exclusivo (XOR), o perceptron não é capaz de modelar, pois são necessárias duas retas para distinguir as classes. Observe na figura a seguir, que as duas classes necessitam de duas retas para separá-las corretamente. A classe 0 é representada pelas bolinhas vazias e a 1 pelas bolinhas cheias, e as retas de separação estão em vermelho.


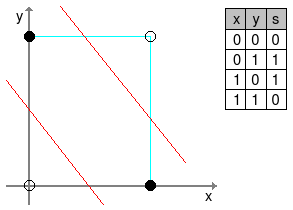
  A solução para esse problema é ampliar a quantidade de neurônios (ou perceptrons). Ao fazermos isto, estamos criando uma rede neural artificial (RNA), onde vários neurônios trabalham em conjunto em busca da solução de um problema.
  Uma rede neural possibilita ao sistema utilizar soluções não-lineares mais complexas para separar as classes. Quanto mais neurônios, melhor é a nossa modelagem.
Redes Neurais Feed Forward   Existem diversos tipos de redes neurais. Entretanto, no nosso curso, aprenderemos apenas sobre as redes neurais do tipo feed forward (alimentação para frente).
  Principais características de uma rede neural do tipo feed forward: Arquitetura da rede   A rede é composta basicamente por:   A figura a seguir apresenta uma rede neural com duas entradas (camada entrada), dois neurônios na camada escondida e um neurônio na camada de saída.


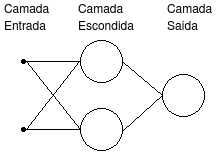
  Apesar das duas entradas não serem neurônios, elas seguem as mesmas regras dos neurônios quanto às conexões aos neurônios da camada seguinte.
  Sabemos que o neurônio recebe N sinais vindos de outros neurônios, realiza o somatório desses sinais multiplicado pelo peso de cada conexão, adiciona o sinal do bias e utiliza uma função de ativação para verificar se envia o sinal adiante.


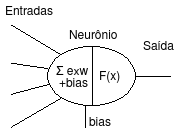
  As funções de ativação normalmente utilizadas em redes neurais são:

  Graficamente:

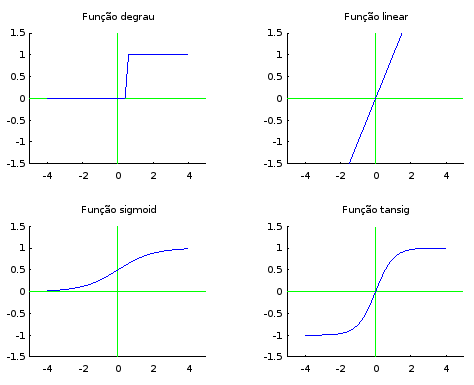
  No perceptron, utilizamos a função de ativação do degrau. Porém, esta função não funciona bem para modelagens não-lineares. Dessa forma, recomenda-se utilizar a função tansig para as camadas escondidas, uma vez que ela possui uma saída contínua em vez de binária. Nos neurônios de saída, normalmente utilizamos a função de ativação linear para problemas de regressão (valores contínuos), pois ela não altera o valor do sinal que chega ao neurônio, e a função de ativação degrau para problemas de classificação (valores binários).
Propagação do sinal   Os sinais sempre se propagam da entrada para a saída. Fazemos o cálculo entre camadas adjacentes, utilizando multiplicação de matrizes.
  Na figura a seguir, assinalamos cada neurônio da camada anterior com uma letra e cada neurônio da camada atual com um número. O peso wA1 conecta o neurônio A com o neurônio 1, o peso wA2 conecta o neurônio A com o neurônio 2, e assim por diante.


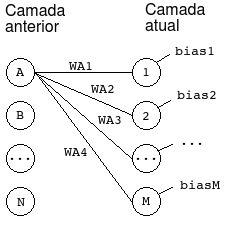
  Utilizamos a seguinte equação matricial para calcular a saída de todos os neurônios da camada atual:


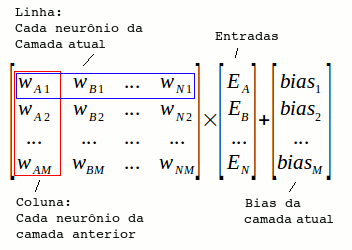
  O vetor de entradas é composto pelos valores de sinais emitidos pelos neurônios da camada anterior (ou da camada de entrada).
  O resultado da multiplicação matricial dos pesos pelas entradas é um vetor coluna, que será somado a outro vetor coluna dos bias da camada atual. Ao final, temos um vetor coluna com todos os sinais que chegam aos M neurônios da camada atual, porém ainda precisam passar pela função de ativação da camada. Dessa forma, aplicamos a função de ativação a cada elemento do vetor resultante.
  Após aplicar a função de ativação, temos os sinais de saída para os neurônios da camada atual, que serão o vetor de entrada para a próxima camada.
Exemplos   O ajustamento de pesos da rede neural não será abordado nesse capítulo. Dessa forma, o treinamento e, consequentemente, o ajustamento de pesos e bias, foram feitos no GNU-Octave.

  Exemplo 1: ou exclusivo - XOR

  Arquitetura da rede: 
Entradas: 2
Camadas escondidas:
  Total: 1
  Número de neurônios: 2
  Função de ativação: tansig
Camada de saída:
  Número de neurônios: 1
  Função de ativação: degrau

  Código: 
5 ' Rede neural - Feed Forward - XOR
6 ' MarMSX 2021
10 SCREEN 0:WIDTH 40:COLOR 15,0,0:KEY OFF
20 NE=2:NH=2:NS=1
30 DIM W1(NH,NE) : DIM E1(NE) : DIM B1(NH) ' Entrada
40 DIM W2(NS,NH) : DIM E2(NH) : DIM B2(NS) ' Camada escondida
50 DIM S(NS) ' Saida
100 '
101 ' Valores entrada
102 '
110 E1(1) = 0
120 E1(2) = 1
200 '
201 ' Inicializa pesos (valores calculados)
202 '
210 W1(1,1)=8.1085 : W1(1,2)=3.2252
220 W1(2,1)=3.6846 : W1(2,2)=2.9790
230 B1(1)=0.38717 : B1(2)=-6.5109
240 W2(1,1)=1.59069 : W2(1,2)=-0.86057
250 B2(1)=-1.4474
300 '
301 ' Classifica
302 '
310 FOR I=1 TO NH : E2(I)=0 :FOR J=1 TO NE
320 E2(I) = E2(I) + W1(I,J) * E1(J)
330 NEXT J : E2(I) = 2 / (1 + EXP(-2 * (E2(I) + B1(I)))) - 1 : NEXT I
340 FOR I=1 TO NS : S(I)=0 :FOR J=1 TO NH
350 S(I) = S(I) + W2(I,J) * E2(J)
360 NEXT J : S(I) = S(I) + B2(I) : IF S(I)>.5 THEN S(I)=1 ELSE S(I)=0
370 NEXT I
400 '
401 ' Imprime resultado
402 '
410 PRINT "Saida:"
420 FOR I=1 TO NS
430 PRINT S(I)
440 NEXT I
  O programa recebe duas entradas na linhas 110 e 120 e as aplica na rede neural. Nesse caso, temos as seguintes entradas: 0 e 1.

  Saída:
  1

  A saída está correta. Agora experimente alterar os valores de entrada nas linhas 110 e 120.

  Rode o programa RN_XOR.BAS contido no pacote desse capítulo. A saída é apresentada a seguir.
E1= 0  E2= 0  Saida: 0
E1= 0  E2= 1  Saida: 1
E1= 1  E2= 0  Saida: 1
E1= 1  E2= 1  Saida: 0
  O que mostra que a rede neural pôde modelar corretamente o ou exlusivo.

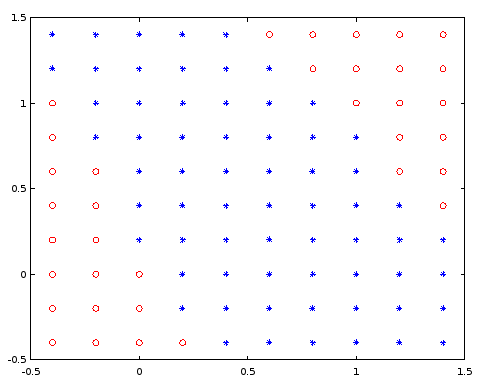
  Veja no gráfico a seguir, a classificação dessa rede para diversos valores de entrada contínuos entre -1,4 e 1,4. A bola vermelha indica a classe 0, enquanto que o asterisco azul indica a classe 1.



  Exemplo 2: flor íris [2]

  Arquitetura da rede: 
Entradas: 2
Camadas escondidas:
  Total: 1
  Número de neurônios: 4
  Função de ativação: tansig
Camada de saída:
  Número de neurônios: 3
  Função de ativação: linear

  Código: 
5 ' Rede neural - Feed Forward - Iris 3 classes
6 ' MarMSX 2021
10 SCREEN 0:WIDTH 40:COLOR 15,0,0:KEY OFF
20 NE=2:NH=4:NS=3
30 DIM W1(NH,NE) : DIM E1(NE) : DIM B1(NH) ' Entrada
40 DIM W2(NS,NH) : DIM E2(NH) : DIM B2(NS) ' Camada escondida
50 DIM S(NS) ' Saida
100 '
101 ' Valores entrada
102 '
110 E1(1) = 1.4
120 E1(2) = 0.2
200 '
201 ' Inicializa pesos (valores calculados)
202 '
210 W1(1,1)=-1.26811 : W1(1,2)=10.54471
215 W1(2,1)=-2.31851 : W1(2,2)=-2.13512
220 W1(3,1)=-0.49873 : W1(3,2)=-0.62087
235 W1(4,1)=1.61826 : W1(4,2)=-10.82781
240 B1(1)=-11.6003 : B1(2)=7.4798 : B1(3)=-1.7431 : B1(4)=10.3022
250 W2(1,1)=-0.0025978 : W2(1,2)=0.5036170 : W2(1,3)=-0.4509608 : W2(1,4)=-0.0029980
255 W2(2,1)=-2.2281652 : W2(2,2)=-0.5020465 : W2(2,3)=0.1524250 : W2(2,4)=-1.7334303
260 W2(3,1)=2.2271598 : W2(3,2)=0.0010528 : W2(3,3)=-0.2051632 : W2(3,4)=1.7328068
265 B2(1)=0.052374 : B2(2)=0.156305 : B2(3)=0.290303
300 '
301 ' Classifica
302 '
310 FOR I=1 TO NH : E2(I)=0 :FOR J=1 TO NE
320 E2(I) = E2(I) + W1(I,J) * E1(J)
330 NEXT J : E2(I) = 2 / (1 + EXP(-2 * (E2(I) + B1(I)))) - 1 : NEXT I
340 FOR I=1 TO NS : S(I)=0 :FOR J=1 TO NH
350 S(I) = S(I) + W2(I,J) * E2(J)
360 NEXT J : S(I) = S(I) + B2(I) : NEXT I
400 '
401 ' Imprime resultado
402 '
410 PRINT "Saida:"
420 FOR I=1 TO NS
430 PRINT S(I)
440 NEXT I
  Obs: este programa é o mesmo que o anterior, onde somente modificamos a arquitetura da rede, as entradas, os pesos, os bias e a função da camada de saída para linear.

  Saída:
  1.001
  -1.144E-03
  -2.461E-04

  Os valores de entrada são a medida de comprimento e largura da pétala de um flor setosa. Entretanto, antes de analisarmos o resultado do programa, vamos responder à seguinte pergunta: por quê três neurônios na camada de saída?
  Quando temos um problema de classificação, é recomendável colocar um neurônio da camada de saída para cada classe que tivermos no conjunto de dados. Vimos no capítulo do perceptron que o conjunto total de iris possui 3 classes: setosa, versicolor e virgínica. Assim, cada neurônio da camada de saída deverá sinalizar com o valor 1 para uma classe correspondente e 0 para as demais. Por exemplo:
  O resultado obtido no programa apresenta o valor 1.001 para S(1), -1.144E-03 para S(2) e -2.461E-04 para S(3). Cada valor desse significa a probabilidade do dado testado pertencer a cada uma das três classes. Observa-se que a maior probabilidade está na classe 1, que é a classe setosa. O programa acertou.
  Para facilitar a visualização da classificação, podemos colocar a função de ativação degrau nos neurônios da camada de saída.

  Se você ainda não percebeu nesse exemplo, as redes neurais são capazes de discriminar mais de duas classes. Aqui, podemos testar se as medidas de comprimento e largura de uma dada flor íris pertence às classes setosa, versicolor ou virgínica.

  Rodando o programa RN_IRIS.BAS contido no pacote desse capítulo, testamos as 150 flores íris de três tipos diferentes. Ao final, o erro de classificação foi de 5 em 150, o que corresponde a 97% de acerto.
Considerações finais   Vimos que é relativamente fácil implementar uma rede neural no MSX, obtendo excelentes resultados.
  O MSX leva aproximadamente 0.5 segundos para classificar cada par de entradas no exemplo do XOR, e 1 segundo para cada par da flor íris, ambas em Basic. Isto significa que é possível utilizar redes neurais mais complexas para classificação ou regressão no MSX, principalmente se desenvolvidas em linguagens como C e Pascal. O problema fica por conta do treinamento, que é lento e exaustivo mesmo nos modernos PCs.



  Referências

  1. Neural Java, Cleuton Sampaio. Editora Ciência Moderna, 2020.
  2. Iris, Repositório de dados da UCI. Em http://archive.ics.uci.edu/ml/index.php


<< Anterior   AI   Próxima >>